Vector is a quantity that besides having a quantitative (large) value also has a direction, for example the amount of speed, force, and moment
Table Of Contents
1. Understanding scalar and vectors
In everyday life, we find a lot of quantities, such as the length of a stick, the volume of a can, the area of a garden, the amount of electric charge, the mass of an object and so on.The quantities are usually expressed by a number accompanied by the unit of amount.Such a large amount, called scalar.
If we move or shift an object (material) in any form, the transfer of the object will meet two elements, namely how far the move and in which direction the object moves.The two elements that affect the transfer of objects are called the vector quantities.So, vectors are quantities that besides having a quantitative (large) value also have directions, for example the amount of speed, force, and moment.
Example:
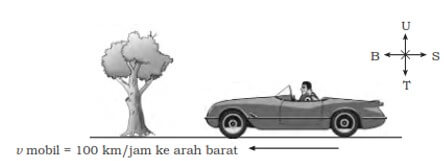
A car drove at a speed of 100 km/h to the west.The event is a form of vector use in everyday life.The vector used has a large 100 km/hour and drove to the west.
2. Drawing and writing vectors
Vector notation and techniques using vector analysis are very useful for explaining science laws and their applications both in the field (dimensions two = R2) and space (dimensions three = R3).Geometrically, vectors can be presented with directed lines.The length of the line segments state the size of the vector and arrows state the direction of the vector.In its presentation, a vector is usually described as a segment or segment of directions as follows:
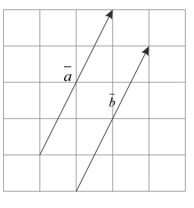
A vector can be given a symbol with one of its members as a representative of the set of lines.The vector in the picture above can be represented by one of the lines, for example $\underline{a}$ or $\overrightarrow{\text{AB}},\text{ }\overrightarrow{\text{CD}}\text{, }\overrightarrow{\text{EF}}$ or others.In the literature there are several symbols for vector representatives, including:
(1) with lowercase letters a, b, c, … (which is printed bold) or $\underline{a}$, $\underline{b}$, $\underline{c}$,…, or $\overline{\text{a}},\text{ }\overline{\text{b}}\text{, }\overline{\text{c}}\text{, }…$
(2) with uppercase, for example $\overrightarrow{\text{AB}}$ or $\underrightarrow{\text{AB}}$, $\overrightarrow{\text{PQ}}$ or $\underrightarrow{\text{PQ}}$, and so on.The arrow that accompanied him to express the direction, for example $\overrightarrow{\text{AB}}$ Intended as a vector representative with a base point A and ended.
Large or length of a vector $\overline{\text{a}}$ can be stated with $\left| \overline{\text{a}} \right|$, while the large vector $\overrightarrow{AB}$ can be stated with $\left| \overrightarrow{\text{AB}} \right|$.
3. Vector room
When the first time vector science was developed, only known vectors in ${{R}^{2}}$ dan ${{R}^{3}}$ Only, but in its development it turns out that more complex problems are obtained so that vectors in the dimensions of 4, 5 or generally developed vectors in the vectors ${{R}^{n}}$ . Geometrically indeed vectors in ${{R}^{4}}$ and so on it is not yet described, but the basis used such as vector operations is still the same as operations on vectors-vectors in ${{R}^{2}}$ dan ${{R}^{3}}$ . The person who first studied the vectors in $Rn$ was Euclidis so that the vectors were on ${{R}^{n}}$ Known as an euclidis vector, while the vector space is called euclidis space.
In this material what we learn is a vector in ${{R}^{2}}$ and vectors at ${{R}^{3}}$. Vectors at ${{R}^{3}}$ is a vector located in the dimensional room three or vectors that have three components namely x, y, z. Meanwhile, vectors at ${{R}^{2}}$ is a vector located in a field or vector with only two components namely x and y.
4. Zero vector
The zero vector is a large vector/zero length (the starting point and end point are the same/coincide) and the direction is not necessarily such as: $$\overrightarrow{AA}=\overrightarrow{O},\overrightarrow{BB}=\overrightarrow{O}$$. In the Cartesian Coordinate System the zero vector is described in the form of a point.In the dimensions of two zero vectors is symbolized by $\overrightarrow{O}=\left( 0 \\ 0 \right)$
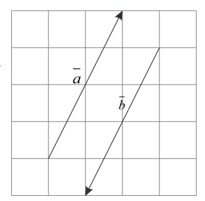
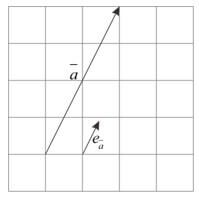
5. Negative vector
Negative vectors from $\overline{a}$ is a vector whose size is the same as the vector $\overline{a}$, but his direction is opposite and written $-\overline{a}$. Look at the picture on the side.Vector $\overline{a}$ align $\overline{b}$ and the same length but the direction is the opposite then $\overline{a}=-\overline{b}$.
6. Unit vector
Unit vectors are vectors that have a length of 1 unit and are denoted as $e$. Unit vector from the vector $\overline{a}$ Defined vectors $\overline{a}$ divided by the vector size $\overline{a}$ alone, which was formulated with ${{e}_{\overline{a}}}=\frac{\overline{a}}{\left| \overline{a} \right|}=\frac{1}{\left| \overline{a} \right|}\overline{a}$
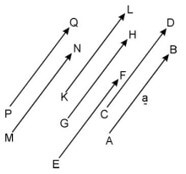
7. The similarity of two vectors
Two vectors $\overline{a}$ dan $\overline{b}$ It is said to be the same when both have large (long) and the same direction.Take a look at the picture in addition.Visible $\overline{a}$ align $\overline{b}$ And the same is the same.Obtain $\overline{a}=\overline{b}$.
