Master the theorem of multiples of 3: rules, proof, examples, and modular arithmetic applications for high school math.

Theorem of Multiples of 3: Rules, Proof, and Applications

1. Introduction

The theorem of multiples of 3 is one of the quick division rules taught in elementary school and often used up to high school level. The rule is simple:

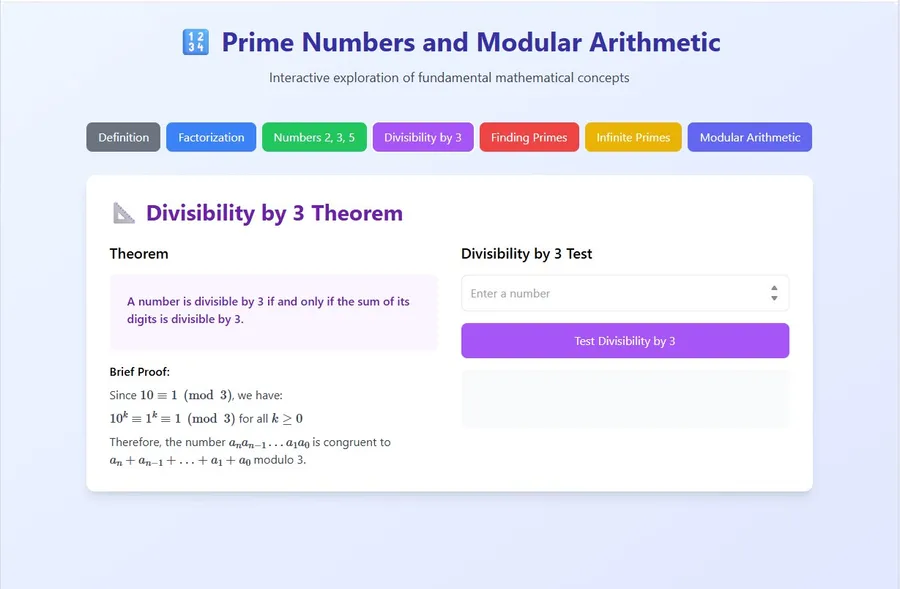
A number is divisible by 3 if the sum of all its digits is divisible by 3.

Although it seems like a quick trick, this rule actually has a strong mathematical basis, especially in the concept of modular arithmetic.

2. Definition of Multiples of 3

Multiples of 3 are all numbers that can be expressed as:

$$3 \times n,\quad n \in \mathbb{Z}$$

Examples: 0, 3, 6, 9, 12, 15, 18, 21, …

3. Rule of Multiples of 3

Theorem Statement:

A positive integer $N$ is divisible by 3 if and only if the sum of its digits is divisible by 3.

4. Proof of the Theorem of Multiples of 3

Suppose $N$ is a number with digits $d_k d_{k-1} \dots d_1 d_0$. Mathematically:

$$N = d_k \times 10^k + d_{k-1} \times 10^{k-1} + \dots + d_1 \times 10^1 + d_0$$

In modulo 3:

$$10 \equiv 1 \ (\text{mod}\ 3)$$

So:

$$10^n \equiv 1^n \equiv 1 \ (\text{mod}\ 3)$$

Therefore:

$$N \equiv d_k + d_{k-1} + \dots + d_1 + d_0 \ (\text{mod}\ 3)$$

This means $N$ and the sum of its digits have the same remainder when divided by 3. If the sum of the digits is divisible by 3, then $N$ is also divisible by 3.

5. Simple Examples

• 123 → 1+2+3 = 6 → divisible by 3 → 123 is divisible by 3.
• 457 → 4+5+7 = 16 → not divisible by 3 → 457 is not divisible by 3.
• 900 → 9+0+0 = 9 → divisible by 3 → 900 is divisible by 3.

6. Variations and Extensions

1. Multiples of 9 The rule is similar to multiples of 3: if the sum of the digits is divisible by 9, the number is divisible by 9.

2. Test for Large Numbers For numbers with hundreds of digits, just keep summing the digits repeatedly until you get a single digit.

3. Relation to Modular Arithmetic

   • $a \equiv b \ (\text{mod}\ 3)$ is used to check the remainder when divided by 3.
   • This rule is a direct application of the property $10^n \equiv 1 \ (\text{mod}\ 3)$.

7. Example Problems and Solutions

Problem 1

Determine whether 5,238 is divisible by 3.

Solution: Sum of digits: 5+2+3+8 = 18 → divisible by 3 → Yes, 5,238 is divisible by 3.

Problem 2

Find all 3-digit numbers between 300–320 that are divisible by 3.

Solution:

• 300 → 3+0+0 = 3 → yes
• 301 → 3+0+1 = 4 → no
• 302 → 3+0+2 = 5 → no
• 303 → 6 → yes Continue, the results: 300, 303, 306, 309, 312, 315, 318.

Problem 3

Prove that 1,111,111 is divisible by 3.

Solution: Sum of digits: 1+1+1+1+1+1 = 6 → divisible by 3 → proven.

8. Independent Exercises

1. Determine whether 789,456 is divisible by 3.
2. Find 5 numbers between 1,000 and 1,020 that are divisible by 3.
3. Prove that 9,999 is divisible by 3.

Short Answer Key:

1. Yes
2. 1,002; 1,005; 1,008; 1,011; 1,014
3. Sum of digits 9+9+9+9 = 36 → divisible by 3.

9. Real-Life Applications

• Dividing goods: Dividing the number of items into equal groups without remainder.
• Input error checking: Cashier systems sometimes check multiples of 3 for code validation.
• Data encoding: Using mod 3 for shift or schedule division.

10. Conclusion

The theorem of multiples of 3 is not just an arithmetic trick, but a beautiful example of how simple mathematics has an elegant formal proof. By understanding this rule, students can quickly check large divisions without a calculator.