Learn the concept of transpose and matrix similarity easily and completely. Find example questions and complete discussions to help you master class 11 mathematics material

A matrix is ​​an arrangement of numbers arranged in rows and columns. Operations on matrices, such as addition, subtraction, multiplication, etc., have special rules.

Previously we learned about matrix concepts and types↝ . This time we will discuss transpose and similarity matrices.

1. Transpose Matrix (Transpose Matrix)

The transpose of a matrix $A$ of order $m \times n$ is a new matrix of order $n \times m$ which is obtained by swapping row elements into column elements and vice versa.

The transpose of a matrix $A$ is denoted by $𝐴^T$

For more clarity, look at the image below: 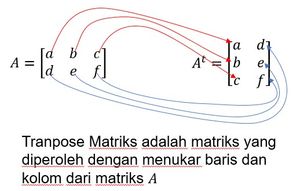Transpose Matrix Example:

If $A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix}$, then $A^T = \begin{bmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{bmatrix}$.

Properties of Matrix Transpose:

  • $(A^T)^T = A$
  • $(A + B)^T = A^T + B^T$
  • $(kA)^T = kA^T$, where $k$ is a constant
  • $(AB)^T = B^TA^T$

2. Similarity of Two Matrices

Definition

Two matrices $A$ and $B$ are said to be equal if and only if:

  1. The orders of matrices $A$ and $B$ are the same.
  2. The elements in the matrices $A$ and $B$ are the same.

Example:

Matrix $A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$ and $B = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$ are the same matrix.

Sample Question

  1. Given the matrix $P = \begin{bmatrix} 2 & -1 \\ 3 & 4 \end{bmatrix}$ and $Q = \begin{bmatrix} 1 & 2 \\ -3 & 4 \end{bmatrix}$. Determine:

    1. $P^T$
    2. $Q^T$
    3. $(P + Q)^T$
    4. Is $P$ the same as $Q$?

  2. If $A$ is a matrix of order $3 \times 2$, determine the order of $A^T$.

Problem Solving

  1. Known matrix:

    • $P = \begin{bmatrix} 2 & -1 \\ 3 & 4 \end{bmatrix}$
    • $Q = \begin{bmatrix} 1 & 2 \\ -3 & 4 \end{bmatrix}$

    Asked:

    1. $P^T$
    2. $Q^T$
    3. $(P + Q)^T$
    4. Is $P$ the same as $Q$?

    Solution ✍️

    1. Finding $P^T$ and $Q^T$

      To find the transpose, we convert rows into columns and vice versa.

      • $P^T = \begin{bmatrix} 2 & 3 \\ -1 & 4 \end{bmatrix}$
      • $Q^T = \begin{bmatrix} 1 & -3 \\ 2 & 4 \end{bmatrix}$

    2. Finding $(P + Q)^T$

      First, we add the matrices $P$ and $Q$:

      $P + Q = \begin{bmatrix} 2+1 & -1+2 \\ 3-3 & 4+4\end{bmatrix} = \begin{bmatrix} 3 & 1 \\ 0 & 8 \end{bmatrix}$

      Then, we find the transpose of the addition result:

      $(P + Q)^T = \begin{bmatrix} 3 & 0 \\ 1 & 8 \end{bmatrix}$

    3. Checking if $P$ is equal to $Q$

      Two matrices are said to be the same if their order and elements are the same. We see that the matrices $P$ and $Q$ have the same order, namely $2 \times 2$. However, the elements are not all the same. So, $P$ is not the same as $Q$.

  2. If $A$ is a matrix of order $3 \times 2$, determine the order of $A^T$.

    Solution ✍️

    If the matrix $A$ has 3 rows and 2 columns, then when it is transposed, the rows and columns will swap. So, the matrix $A^T$ will have 2 rows and 3 columns.

    So, the order of $A^T$ is $2 \times 3$.

Extra Practice Questions

  1. Given the matrix:

    • $A = \begin{bmatrix} 1 & -2 & 3 \\
      4 & 0 & -5 \end{bmatrix}$
    • $B = \begin{bmatrix} 2 & 1 \\
      -1 & 3 \\
      0 & 2 \end{bmatrix}$

    Determine:

    • $A^T$
    • $B^T$
    • $(A + B)^T$ (note: the addition operation A + B cannot be performed because the order of the matrices is different)
    • $(AB)^T$ (if AB matrix multiplication can be performed)

  2. Given the matrix $C = \begin{bmatrix} x & 2 \\ 3 & y \end{bmatrix}$ and $D = \begin{bmatrix}4 & 2 \\3 & 1 \end{bmatrix}$. If $C = D^T$, determine the values ​​of $x$ and $y$.

  3. Prove that for every square matrix $A$, $(A^T)^T = A$ holds.

  4. Given the matrix $E = \begin{bmatrix} a & b \\ c & d \end{bmatrix}$. If $E^T = E$, what kind of matrix is ​​called a symmetric matrix? Give an example of a symmetric matrix of order $3 \times 3$.

  5. Given the matrix $F = \begin{bmatrix}a & b \\-b & a\end{bmatrix}$. If $F^T = -F$, what kind of matrix is ​​called a skew-symmetric matrix? Give an example of a skew-symmetric matrix of order $2 \times 2$.