Function Limit Concept | Example Questions and Complete Discussion

Bakhtiar Rifai• 21 Mar 2025

#Calculus #High school mathematics #Function Limits

Find a simple explanation of function limits in mathematics. Complete with example questions and visualizations that are easy to understand in high school mathematics lessons

Have you ever wondered, “What are function limits and why should we study them?” The concept of limits may sound foreign and complicated at first, but it is actually very important in mathematics. Limits are a basic concept that is the foundation for understanding advanced concepts such as derivatives and integrals.

We often hear the word approaching, for example, the speed of the car is approaching 160 km/hour. Well, this word approaching in mathematics is called limit.

In this article, we will study the limits of functions that are usually studied at high school level. Function limits: We learn about limits of algebraic functions and limits of trigonometric functions. Before discussing further, we will study the meaning of limits in depth and determine the limit value first.

What is Function Limit?

In simple terms, function limit is the approach value around a certain point, whether approaching from the left or approaching from the right of that point. Imagine a graph of a function. As we approach a certain point on the graph, the function value will get closer to a certain value. This value is called the limit.

General form of Function Limit Notation

$\lim \limits_{x\rightarrow a} f(x) = L$

$\lim$ : Abbreviation for “limit”.
$f(x)$ : The function we are looking at.
$x \rightarrow a$ : Meaning “x approaches a”.
$L$ : The value f(x) approaches as x approaches a.

How to read function limit notation:

$\displaystyle \lim_{x \to a } f(x) = L$ reads as the limit of the function $f(x)$ for $x$ approaching $a$ equal to $L$ .

For more details, pay attention to the following illustration:

Suppose there is a function $𝑓(𝑥) = x+2$ . Determine the value of $\lim\limits_{x \to 2} f(x)$ if it exists! To determine the limit of the algebraic function at $𝑥 \to 𝑎$ we can use a table like the following. If we substitute the 𝑥 values from the left then the value will be close to 4, whereas if we substitute the x values from the right then the value will be close to 4 too. This can be written as follows.

$\lim\limits_{x \to 2^+}x+2=4$ dan $\lim\limits_{x \to 2^-}x+2=4$ maka $\lim\limits_{x \to 2}x+2=4$ .

If presented in a graph like the following

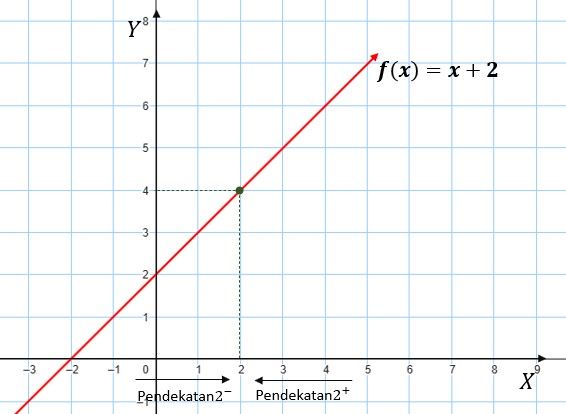
So, the value of $\lim\limits_{x \to 2^+}x+2$ is 4

Function Limit Definition

Mathematically the limit can be defined as follows.

Let $f$ be a function $f : R \rightarrow R$ and let $L$ and $a$ be real numbers.

$\displaystyle \lim_{x \to a } f(x) = L$ if and only if $f(x)$ approaches $L$ for all $x$ approaches $a$ .

How to read function limit notation: $\displaystyle \lim_{x \to a } f(x) = L$ reads as the limit of the function $f(x)$ for $x$ approaching $a$ equal to $L$ .

Function Limit Conditions

A limit is said to exist if the limit has the same left limit and right limit.

If the function 𝑓(𝑥) is defined on the open interval I, then:

$\lim \limits_{x \to a} f(x) = L$ (exists) if and only if $\lim \limits_{x \to a^+} f(x) = L$ and $\lim \limits_{x \to a^-} f(x) = L$
Jika $\lim \limits_{x \to a^+} f(x) = L_1$ dan $\lim \limits_{x \to a^-} f(x) = L_2$ dimana $𝐿_1 ≠ 𝐿_2$ maka $\lim \limits_{x \to a} f(x)$ tidak ada

To understand better, take a look at the following example…

Determine the Function Limit Value

To determine the limit value of a function, there are several ways:

Numerical Methods
Substitution
Factoring
Kali is his friend
Using Derivatives

In terms of basic mathematical concepts, how to work on existing mathematical problems the limit, just replace/substitute the variable 𝒙 into a number approached by 𝑥.

Sample Question 1

Determine the limit f(x) for the function $f(x) = \begin{cases}2x^2 &\text{jika }x\leq 1 \\ 2x-1 &\text{jika } x > 1\end{cases}$ for $x$ approaches 1 if it exists?

Solution ✍️

Function description:
If the value of $x \leq 1$ then $f(x) = 2x^2$ applies
If the value of $x > 1$ then $f(x) = 3x + 1$ applies
Table of approximations from the left and from the right for $x$ approaching 1.
Analysis of left limit and right limit results. The table above shows: $\lim \limits_{x \to 1^-} f(x) = 2$ dan $\lim \limits_{x \to 1^+} f(x) = 4$ (left limit ≠ right limit), so $\lim \limits_{x \to 1} f(x)$ does not exist.

For more details, look at the following image.

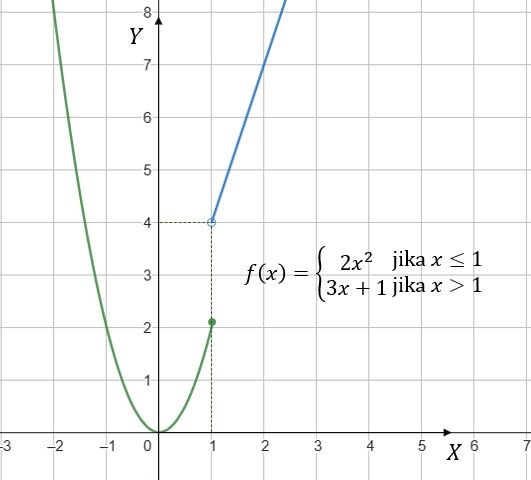
So, the function $f(x) = \begin{cases}2x^2 &\text{if }x\leq 1 \\ 2x-1 &\text{if } x > 1 \end{cases}$ until $x$ approaches 1 has no limit.

Example Question 2

Diketahui $\lim\limits_{x \to 1} \frac{5x^3+7x^{14}+6}{8x^9+4x^7-6}$ What is the result of the limit value from the data above?

Solution ✍️

In the limit above, to find the limit value, you just need to substitute or replace the variable 𝑥 with the number 1, so that the limit result becomes $\begin{align*}\lim\limits_{x \to 1} \frac{5x^3+7x^{14}+6}{8x^9+4x^7-6} &=\frac{5.1^3+7.1^{14}+6}{8.1^9+4.1^7-6} \\ &= \frac{5+7+6}{8+4-6} \\ &=\frac{18}{6} =3\end{align*}$ So, the limit value is 3

That’s the article, hopefully it will be easier for you to understand the concept of function limits and be motivated to continue studying mathematics. Next we will learn about the properties of function limits.

Keep the spirit Okay…