Learn about the Limit of a Function, one of the fundamental concepts in calculus (differential and integral) and high school mathematics.
📘 What is a Function Limit in Mathematics?
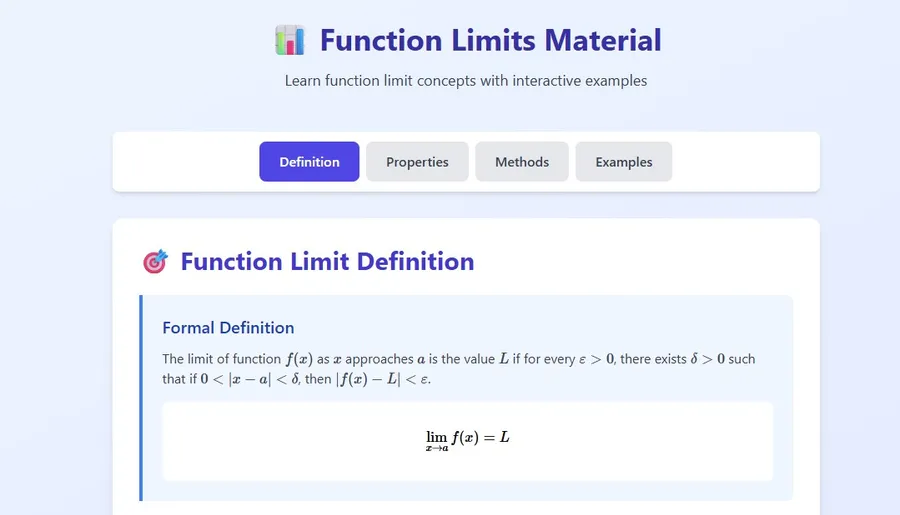
A function limit is one of the basic concepts in calculus and high school mathematics that describes the value a function approaches as the variable gets close to a certain point. Limits are a crucial foundation for learning derivatives (differential) and integrals.
📐 Writing the Limit Notation
In mathematics, a limit is written as:
$$ \lim_{x \to a} f(x) = L $$
Meaning:
As $x$ approaches $a$, the function $f(x)$ approaches the value $L$.
A limit can exist even if the function is not defined at that point. This is what distinguishes the value of a limit from the value of the function.
🔄 Simple Example of a Function Limit
For example, the function:
$$ f(x) = x + 2 $$
Then:
$$ \lim_{x \to 3} f(x) = \lim_{x \to 3} (x + 2) = 5 $$
Explanation: As $x$ approaches 3, the function value approaches 5. This is the simplest example of a linear function limit.
📊 Approaching Limits Using a Table
If you want to understand limits numerically, you can look at them in the form of an approach table:
$$ \lim_{x \to 2} x^2 $$
| $x$ | $f(x) = x^2$ |
|---|---|
| 1.9 | 3.61 |
| 1.99 | 3.9601 |
| 2.01 | 4.0401 |
| 2.1 | 4.41 |
It can be seen that:
$$ \lim_{x \to 2} x^2 = 4 $$
🧭 Left-Hand and Right-Hand Limits
In calculus, we know:
Left-hand limit:
$$ \lim_{x \to a^-} f(x) $$
Right-hand limit:
$$ \lim_{x \to a^+} f(x) $$
🔁 If Both Are Equal:
$$ \lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x) = L \Rightarrow \lim_{x \to a} f(x) = L $$
❌ Example of a Nonexistent Limit
Consider the following function:
$$ f(x) = \begin{cases} 1, & x < 0 \\ 2, & x \geq 0 \end{cases} $$
- $\lim_{x \to 0^-} f(x) = 1$
- $\lim_{x \to 0^+} f(x) = 2$
Because the left and right limits are different, then:
$$ \lim_{x \to 0} f(x) \text{ does not exist (limit does not exist)} $$
📝 Example Problems on Function Limits and Their Solutions
Problem 1:
$$ \lim_{x \to 3} (2x - 5) = ? $$
Solution:
$$ 2(3) - 5 = 1 $$
Problem 2:
$$ \lim_{x \to 1} \frac{x^2 - 1}{x - 1} \Rightarrow \frac{(x - 1)(x + 1)}{x - 1} = x + 1 \Rightarrow 2 $$
Problem 3:
$$ \lim_{x \to 2} \frac{x^2 - 4}{x - 2} \Rightarrow \frac{(x - 2)(x + 2)}{x - 2} = x + 2 \Rightarrow 4 $$
📌 Conclusion: What is a Function Limit?
- A limit shows the direction a function approaches, not the function’s value at that point.
- A limit can still be calculated even if the function is not defined at that point.
- Understanding limits is very important as a foundation for derivatives and integrals in grades 11 and 12 of high school.
Whats next?????