Arithmetic Series and Sequences, Formulas and Their Applications

Learn the basic concepts of arithmetic sequences and series. This article explains what arithmetic sequences and series are, their formulas, and how they are applied in everyday life.

Arithmetic sequences and series are two important mathematical concepts frequently used in various contexts. You’ve probably learned about sequence patterns since junior high school. In this article, we’ll explain the definitions, formulas, and some applications of these two concepts. In addition to arithmetic sequences and series, we’ll also discuss geometric sequences and series. Please read the article Geometric Sequences and Series↝ . For more details, let’s look at the explanations of each below.

1. Understanding Number Lines

A number sequence is a sequence of numbers arranged in a specific pattern or order based on a specific rule. This sequence can consist of integers, real numbers, or other types of numbers and is usually separated by a comma. Each number in the sequence is called a term, and each term has a position in the sequence that indicates its order.

In a number sequence, the rules or patterns used to generate each term are usually consistent or involve a specific mathematical relationship between successive terms. This pattern can be addition, subtraction, multiplication, division, or other mathematical relationships.

Example of a Number Line

Here are some examples of number sequences with different patterns.

a. 1, 2, 3, 4, 5,….
b. 2, 4, 6, 8, 10,….
c. 14, 11, 8, 5, 2,….
d. 2,– 2, 2, – 2, 2, – 2,….

In the example above, the numbers in a,b,c,d,e have certain rules so it is called a series of numbers.

a. $\underbrace{1, 2}_{+1} \underbrace{, 3 }_{+1} \underbrace{, 4 }_{+1} \underbrace{, 5 }_{+1} , ….$
b. $\underbrace{2, 4}_{+2} \underbrace{, 6 }_{+2} \underbrace{, 8 }_{+2} \underbrace{, 10 }_{+2} , ….$
c. $\underbrace{14, 11}_{-3} \underbrace{, 8 }_{-3} \underbrace{, 5 }_{-3} \underbrace{, 2 }_{-3} , ….$
d. $\underbrace{2, -2}_{-4} \underbrace{, 2 }_{+4} \underbrace{, -2 }_{-4} \underbrace{, 2 }_{+4} , ….$

Notes

• Each number on the number line is called a quarter (U)
• The first quarter is denoted by $U_1$ or $a$
• The second quarter is denoted by $U_2$
• The third term is denoted by $U_3$
• The nth quarter is denoted by $U_n$ where $n ∈ A$ (Natural number)

2. Arithmetic Sequence

An arithmetic sequence is a sequence of numbers where the difference between two consecutive terms is the same or constant.

Example:
a. 3, 8, 13, 18, ….
b. 10, 7, 4, 1, ….

In the example above, the difference between two consecutive terms remains constant.

a. $\underbrace{3, 8}_{+5} \underbrace{, 13 }_{+5} \underbrace{, 18 }_{+5} \underbrace{, 5 }_{+1} , ….$
b. $\underbrace{10, 7}_{-3} \underbrace{, 4 }_{-3} \underbrace{, 1 }_{-3} \underbrace{, 10 }_{+2} , ….$

The difference between two consecutive terms is called the difference or is symbolized by the letter $d$.

To determine difference, use the formula:

$d = U_2 - U_1$ $d = U_3 - U_2$ $d = U_4 - U_3$ .
.
.
$d = U_n - U_{n-1}$

If the first term = $a$ and the difference = $d$, then in general the Arithmetic sequence those are: $$\begin{matrix}U_1, & U_2, & U_3, & U_4, & & U_n \\ a, & a+d, & a+2d, & a+3d, & \cdots, &a+(n-1)d \end{matrix}$$

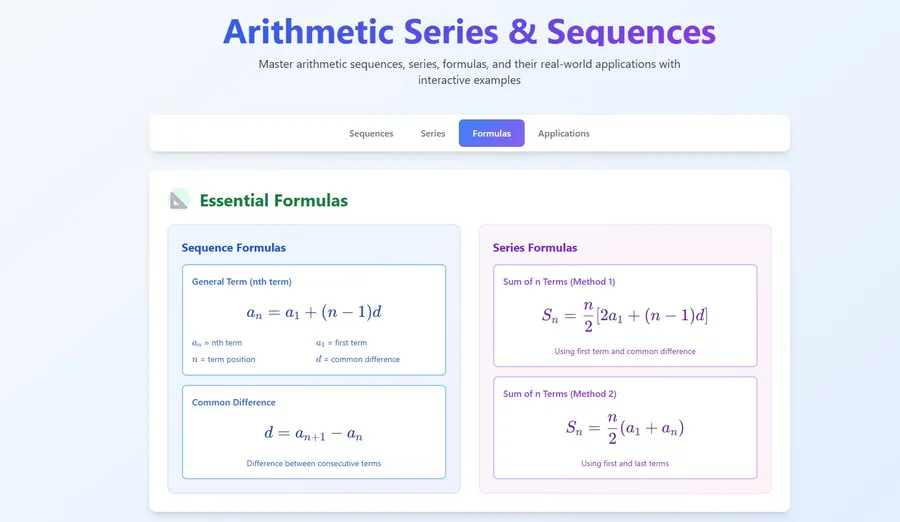
So the formula for the nth term of an arithmetic sequence is $$U_n=a+(n-1)d$$ With :
$U_n$ = nth Quarter
$a$ = First quarter
$d$ = difference or variance

Example of Arithmetic Sequence Problems

1. From rows $3, 5, 7, 9, 11, \cdots$ the $21$ quarter is…

   Solution ✍️

   From rows $3, 5, 7, 9, 11, \cdots$ we get
   first term $a=3$ and
   difference $d=5-3=2$ or $d=11-9=2$.

   The 21st term is:

   $$\begin{align*} U_{n} &= a+\left( n-1 \right)d \\ U_{21} &= 3+\left( 21-1 \right)(2) \\ &= 3+\left( 20 \right)(2) \\ &= 3+40 =43 \end{align*}$$

   $\therefore$ So, the $21$ quarter of the row $3, 5, 7, 9, 11, \cdots$ is $43$

2. An arithmetic sequence is known to have a 6th term of $-4$ and a 9th term of $-19$, so determine the 11th term!

   Solution ✍️

   Notified:

   $𝑈_{6} = -4$
   $𝑈_{9} = -19$

   Asked: $𝑈_{11} = \cdots ?$

   Answer:

   The $n$ term formula is $U_{n} = a+\left( n-1 \right)d$, we get: $$\begin{align*} U_{6} &= -4 & \text{}\\ a+5d &= -4 & \cdots\text{pers (1)}\\ U_{9} &= -19 & \text{}\\ a+8d &= -19 & \cdots\text{pers (2)}\\ \end{align*}$$

   From the two equations above we get:

   • find the value of d
     $$\begin{align*} a+5d &= -4 \\ a+8d &= -19\ (-)\\ \hline -3d= 15 \\ d= -5 \end{align*}$$
   • substitute $d=-5$ into equation (1) $$\begin{align*} a+5d &= -4 \\ a+8(-5) &= -19\\ a-40 &= -19\\ a &= 21 \end{align*}$$
   • search for $U_{11}$ $$\begin{align*} U_{11}= a+10d \\ &= 21+10(-5) \\ &= 21-50=-29 \end{align*}$$

   $\therefore$ So, the 11th term is -29.

Practical Logic The difference is the large term minus the small term, then the result is divided by the difference between the index of the large term minus the index of the small term. $$d=\frac{U_q-U_p}{q-p}$$

Example

If $𝑈_3 = 24$ and $𝑈_8 = 54$ are known, determine the 15th quarter of the row!

Practical logic steps: The 15th term is the 8th term plus 7 differences. So, $$\begin{align*}𝑈_{15} &= 𝑈_8 + 7𝑏\\&= 54 + 7 \left( \frac{54−24}{8−3} \right)\\&= 54 + 7(6)\\&= 54 + 42\\&= 96\end{align*}$$

3. Arithmetic Series

Arithmetic Series is the sum of all the terms in an arithmetic sequence.

If the arithmetic sequence is $U_1, U_2, U_3, \cdots, U_n$ then deret aritmetikanya $U_1+U_2+ U_3+ \cdots+ U_n$ dan denoted by $S_n$.

Formula for the Sum of the First n Terms of an Arithmetic Series $$S_n=\frac12n(a+U_n)$$ or $$S_n=\frac12n(2a+(n-1)d)$$

with:
$S_n$ = Sum of the first n terms of an arithmetic series $U_n$ = nth term of arithmetic series
$a$ = first quarter
$d$ = misery
$n$ = number of terms

Example of Arithmetic Series Problems

1. Determine the sum of the first 20 terms of the arithmetic series 3+7+11+…

   Solution ✍️

   From the series 3+7+11+… we get $a=3 \\ d=7-3=4$

   then substitute into the formula $S_n$

   $$\begin{align*}S_n&=\frac12n(2a+(n-1)d)\\ S_{20}&=\frac12{20}(2(3)+(20-1)4)\\ S_{20}&=10(6+19(4))\\ S_{20}&=10(6+76)\\S_{20}&=10(82)\\ S_{20}&=820\\ \end{align*}$$

   So, the sum of the first 20 terms is 820.

2. Determine the result of $5 + 7 + 9 + 11 + \cdots + 41$ !

   Solution ✍️

   From the form $5 + 7 + 9 + 11 + \cdots + 41$ it is known that it is an arithmetic series so that $a=5\\d=2\\U_n=41$
   • then find the number of terms (n) $$\begin{align*} U_{n}= a+\left( n-1 \right)d \\ 41 &= 5+\left( n-1 \right)(2) \\ 41 &= 5+ 2n-2 \\ 38 &= 2n\\ n &= 19 \end{align*}$$
   • substitute $n=19$ into $S_n$ to find the sum of the first n terms $$\begin{align*} S_{n}&= \dfrac{n}{2} \left( a+U_{n} \right) \\ S_{19}&= \dfrac{19}{2} \left( 5+ 41 \right) \\ &= \dfrac{19}{2} \left( 46 \right) \\ &= 23 \times 19 = 437 \end{align*}$$

   So, the result of $5 + 7 + 9 + 11 + \cdots + 41=437.$

3. Determine the sum of all odd numbers between 10 and 200!

   Solution ✍️

   The sum of odd numbers between 10 and 200 can be written in a series as following $$11 + 13 + 15 + 17 + \cdots +199$$ The series above forms an arithmetic series with $a=11\\d=2\\U_n=199$
   • then find the number of terms (n) $$\begin{align*} U_{n}&= a+\left( n-1 \right)d \\ 199 &= 11+\left( n-1 \right)(2) \\ 199 &= 11+ 2n-2 \\ 190 &= 2n\\ n &= 95 \end{align*}$$
   • substitute $n=95$ into $S_n$ to find the sum of the first n terms $$\begin{align*} S_{n}&= \dfrac{n}{2} \left( a+U_{n} \right) \\ S_{95}&= \dfrac{95}{2} \left( 11+ 199 \right) \\ &= \dfrac{95}{2} \left( 210 \right) \\ &= 95 \times 105 = 9975 \end{align*}$$

   So, the sum of all odd numbers between 10 and 200 is 9975

4. Application of Geometric Sequences and Series

Here are some applications of geometric sequences and series, but there are actually many more. Mathematics is inseparable from real life.

1. An employee at a state-owned enterprise received a salary of 3.2 million in 2020. Then it gets a fixed salary increase every 2 years. If the Officer earns a salary of 4 Million in 2028. Determine

   • a. How much is the nominal difference in salary increases every 2 years?
   • b. Determine how much salary was received in 2016?

   Solution ✍️

   Notified:

   2020 salary of 3.2 Million $\rightarrow U_1=3.2$ increase every 2 years until in 2028 experience 4 times increase then $n=4+1=5$
   2028 salary of 4 Million $\rightarrow U_5=4$

   Asked:

   • a. salary difference every 2 years $\rightarrow d=\cdots?$
   • b. salary in 2016?

   Answer

   • a. find $d$ with the $U_n$ formula $$\begin{align*} b&=\frac{U_q-U_p}{q-p}\\b&=\frac{U_5-U_1}{5-1}\\b&=\frac{4-3,2}{5-1} \\ b&=\frac{0,8}{4}\\b&=0,2\text{ juta}\end{align*}$$ So, the salary difference every 2 years is 0.2 million or 200,000

   • b. the salary in 2016 is the same as the salary in 2020 minus 2 times the increase until $$Salary = U_1-2d=3,2-2(0,2)\\=3,2-0,4=2,8\text{ million}$$

     So, the salary in 2016 was 2.8 million.

2. 2019 National Examination Mathematics and Natural Sciences Questions A laying hen farmer records the number of eggs produced over 12 days. Each day, the number of eggs produced increases by 4. If the first day the number of eggs produced is 20, the total number of eggs produced over 12 days is…
   (A) 480
   (B) 496
   (C) 504
   (D) 512
   (E) 520

   Solution ✍️

   The daily increase in eggs is the same, which is in accordance with the concept of an arithmetic series. With the first term $a=20$ and the increase $d=4$, the series is $20+24+28+\cdots$ and the sum of the first $12$ terms is:

   $$\begin{align*} S_{n} & = \dfrac{n}{2} \left(2a+(n-1)d \right) \\ S_{12} & = \dfrac{12}{2} \left(2(20)+(12-1)(4) \right) \\ & = 6 \left(40+44 \right) \\ & = 6 \left(84 \right) =504 \end{align*}$$

   $\therefore$ The appropriate choice is $(C) 504$

   So, that concludes the topic on arithmetic sequences and series. There are many problems related to arithmetic sequences and series. You can develop your own.