Arithmetic Sequence: Understanding, Formula, and Examples of Questions

Material about the Arithmetic Row of Class 10 Phase E, the nth term formula Example because the problem is discussed in full in this article!

Arithmetic sequences, also known as arithmetic sequences, specifically discuss groups of numbers that follow a specific pattern. The material we will study in arithmetic sequences includes sequences, intercalations, and middle terms. In addition to arithmetic sequences, we will also discuss geometric sequences, arithmetic series, and geometric series. Please read the article.

Line of Numbers

Pay attention to the number pattern: 4, 6, 8, 10, ….

If you observe more closely, the number patterns above are arranged according to certain rules.

Such a number pattern is called a number line.

Example : Here are some example lines!

1. Row of odd numbers: 1, 3, 5, 7, ….
   Information :
   1st quarter (first quarter) is 1 ($U_1 = 1$),
   2nd quarter (second quarter) is 3 ($U_2=3$),
   the 3rd quarter (third quarter) is 5 ($U_3=5$),
   and so on….
2. Line of even numbers: 2, 4, 6, 8, ….
3. Any row: 1, 5, 3, -2, 5, 7, …

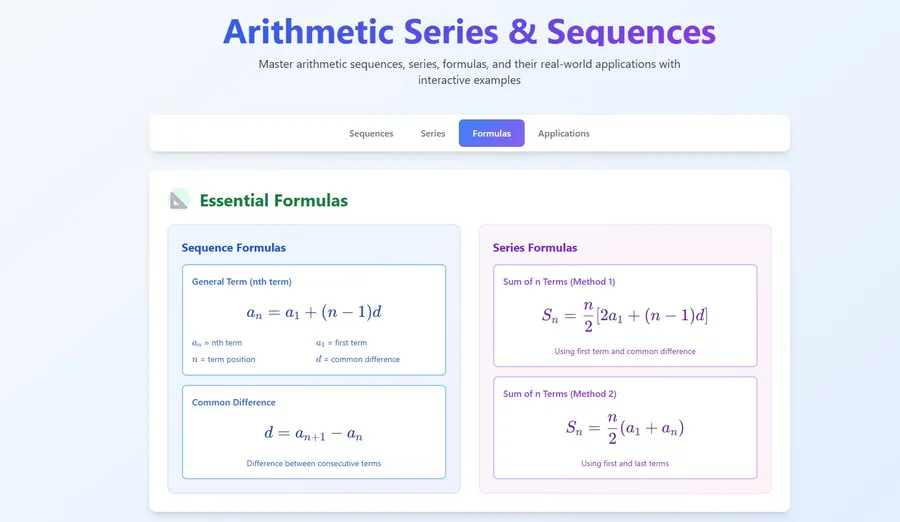
Arithmetic Sequence

Example:

1. Determine the 101st term of the arithmetic sequence -1, 3, 7, 11, 15, ….? Solution:

   • from the line obtained $a = -1$ and $d = 7-3 = 4$
   • Determines the 101st quarter with $U_n = a + (n-1)d$
     $U_{101} = a + (101-1)d = -1 + 100 \times 4 = -1 + 400 = 399$

   So, the 101st term is 399 ($U_{101} = 399$).

2. The 3rd term and the 6th term of a consecutive arithmetic series are known as 9 and 18. Determine the value of the 11th term and the formula of the nth term!
   Solution:

   • Known $U_3 = 9$ and $U_6 = 18$
     To determine the value of a term in a sequence, we need the value of $a$ and its difference ($d$) by explaining the known terms.
   • The formula $: U_n = a+ (n-1)d$
     $$U_6 = a+(6-1)d \\ \rightarrow 18= a + 5b \\ \rightarrow a + 5d = 18 \text{…. pers(i)}$$
     $$U_3 = a+(3-1)d \\ \rightarrow 9= a + 2b \\ \rightarrow a + 2d = 9 \text{…. pers(ii)}$$

• Determine the values of $a$ and $d$ by eliminating equations (i) and (ii) $$\begin{array}{cc}a + 5d = 18 & \\a + 2d = 9 &- \\\hline3d = 9 & \\d = 3 &\end{array}$$
  Pers(ii) : $a + 2d = 9 \rightarrow a + 2(3) = 9 \rightarrow a = 3$
• Determine the formula for the $n$th term $$\begin{align*} U_n &= a+(n-1)d \\ U_n&= 3 + (n-1)3 \\U_n&= 3+3n-3 \\U_n&=3n \end{align*}$$
  So, the $n$ term formula is $U_n=3n$.
  • Determines the 11th quarter
    $U_{11} = 3(11) =$33
    So, the 11th term is 33.

3. An employee at a state-owned enterprise received a salary of 3.2 million rupiah in 2020. He then received a fixed salary increase every 2 years. If the employee receives a salary of 4 million rupiah in 2028, determine:

• a. How many rupiah is the nominal difference in salary increases every 2 years?
• b. Determine how much salary was received in 2016?